好好的链表怎么就有环了！

发表于 | 分类于 | 阅读次数:

什么是有环的链表

今天我们来说下有环的单链表。什么是有环的链表呢？我们都知道，正常单链表最后一个节点的next指针指向的是NULL，但有环的链表就不一样了，它把尾节点的next指针指向了链表中的其他节点（可以是头节点，也可以是其他任何节点）。基本就长下面这样：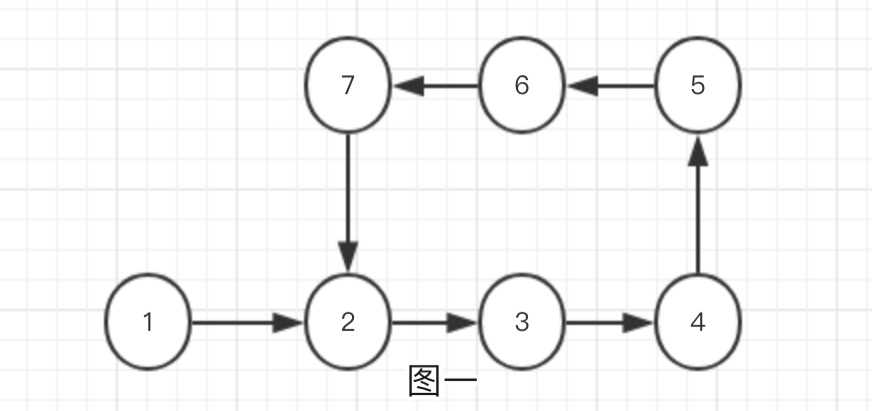

我是萌萌的环形链表
如上图，本应是尾节点的7号节点却指向了2号节点，这样一来就让链表中存在了环。

问题

链表中有环以后呢，那么问题就来了。
我们该如何判断一个链表是否存在环？如果存在我们又如何寻找链表中环的入口呢？如图一，环的入口是2号节点。下面我们就来一一解决这两个问题。

是否存在环

首先说第一个问题，我们讲解的范围仅限于单链表，如何判定其是否存在环？

一般的思路

设置两个快慢指针：fast、slow，都指向链表头。slow一次向前移动一步，fast移动两步，如果两者都没到NULL（有环链表也走不到NULL），而且fast和slow相遇了，则说明链表有环。因为两者的步长不同，如果链表有环，则二者必然会相遇，就是早晚的事。代码就不贴了，注意空链表的特殊情况即可。

另一种思路

在C++中有一种STL是map，在这里我们利用map的特性来解决这个问题。思路就是：初始化一个键为链表节点指针，值为int的一个map对象，从链表头开始遍历，每经过一个节点就把以该节点指针为键对应的值置1，因为map在初始化时默认值是0；然后在遍历的过程中如果比较出键对应的值为1的则说明链表有环。
这个思路有点想哈希的思想，给每个指针一个对应值，看是否有重复。代码如下：

  • 链表节点结构：
1
2
3
4
5
typedef struct ListNode {
    int m_value;
    ListNode *p_next;
    ListNode(int x): m_value(x), p_next(NULL) { }
}Link;
  • 实现：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
bool hasCycle(Link *head) {
	if (head == NULL)
		return false;

	Link *cur = head;

	map<Link *, int> mm;
	while (cur)
	{
		if (mm[cur] == 0)  // default value of map's int type value is 0
			mm[cur] = 1;
		else
			return true;
		cur = cur->p_next;
	}
	return false;
}

这样就可以判定链表中是否有环了。

寻找环的入口

接下来我们来说第二个问题，如何寻找环的入口？这个问题稍微麻烦一点，要先找到fast和slow指针相遇节点meetnode，之后meetnode和头节点一起走再相遇的节点即是环的入口。具体的证明过程就不详细说了，有兴趣的朋友可以看一下有环链表的相关证明，上面很详细的解释了这个结论的来由。知道了结论，代码写起来就很简单了：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
// 找到快慢指针的相遇节点
Link *findSlowAndFastMeetNode(Link *head) {
    Link *slow = head;
    Link *fast = head;

    while (fast != NULL)
    {
        slow = slow->p_next;
        fast = fast->p_next->p_next;

        if (slow == fast)
            return slow;
    }
    return NULL;
}

// 找到环的入口节点
Link *findCycleEntryNode(Link *head, Link *meetNode) {
    if (meetNode == head)
        return meetNode;
    Link *cur = head;
    while (1)
    {
        cur = cur->p_next;
        meetNode = meetNode->p_next;
        if (cur == meetNode)
            return cur;
    }
}

  • 测试代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
    int main()
{
    int arr[] = {1,2,3,4,5,6,7};
    Link *list1= createALinklist(arr, 7);

    Link *cur = list1;  // make list1 a cycle linklist.
    while (cur->p_next)
        cur = cur->p_next;
    cur->p_next = list1->p_next;

    Solution s;
    bool isCycleLinkList = s.hasCycle(list1);

    if (isCycleLinkList)
    {
        cout << "It's a cycle linklist." << endl;
        Link *meetNode = s.findSlowAndFastMeetNode(list1);
        Link *enrtyNode = s.findCycleEntryNode(list1, meetNode);
        cout << "entry node is " << enrtyNode->m_value << endl;
    }
    else
        cout << "It's not a cycle linklist." << endl;



    return 0;
}

执行结果：
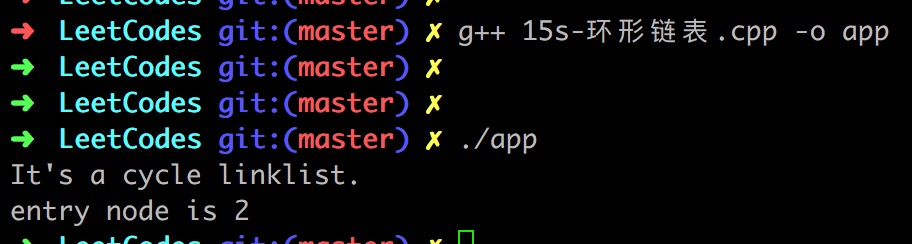
cyclelist-result

由于此代码是提交到Leetcode的，所以把上面几个方法封装到了一个名为Solution的类中，关于链表的创建等基础知识请看我的这篇博客你想要了解的单链表。

关于有环链表的内容今天就说到这里了，有任何问题欢迎讨论！

参考

链表问题集锦
环形链表相关证明