二叉搜索树初探（BST）

发表于 | 分类于 | 阅读次数:

前言

今天来说说经典数据结构之一，二叉搜索树（BST）。
在学习过链表后，再来看二叉树的实现会轻松不少，因为都包含了很多指针操作，同为通过指针指向连接起来的数据结构。建议先把链表吃透，再来看树的实现。

什么是二叉搜索树

二叉搜索树（Binary Search Tree），简称BST，也称为二叉搜索树、有序二叉树或排序二叉树，是指一棵空树或者具有下列性质的二叉树：

1、若任意节点的左子树不空，则左子树上所有节点的值均小于它的根节点的值；
2、若任意节点的右子树不空，则右子树上所有节点的值均大于它的根节点的值；
3、任意节点的左、右子树也分别为二叉查找树；
4、没有键值相等的节点。

下图是否是一颗二叉搜索树呢？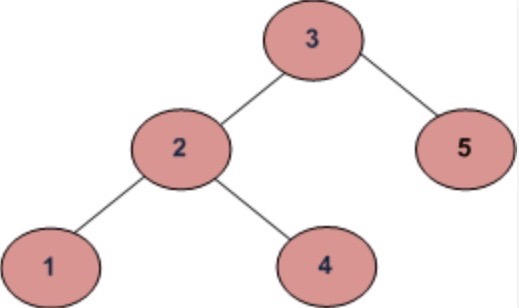

答案是否，因为左子树的最大节点4比根节点3要大，不符合性质1，这个在接下来的如何判断是否为BST中还会讨论到。
二叉查找树相比于其他数据结构的优势在于查找、插入的时间复杂度较低。平均查找复杂度为 O(log n)，查找的效率和树的高度成正比，在最坏情况下为O(n)，这时二叉树退化成一条线。
下面就和我开始一起构建一颗二叉搜索树吧！

二叉搜索树的方法们

BST的方法包括创建、查找、插入、删除和左旋右旋等，今天主要说说前几项。

BST节点的结构

1
2
3
4
5
6
7
class binaryTreeNode 
{
public:
	int item;  // 节点内容
	binaryTreeNode *l_child, *r_child;  // 左孩子和右孩子的指针
	binaryTreeNode(int item):item(item),l_child(NULL),r_child(NULL) { }
};

这里为了方便讲解，暂定二叉树的节点元素为int类型，实际开发中一般会换成特定的结构体。

定义一个BST类

为了方便以后添加树的新方法，定义一个名为binaryTree的类，如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#include <iostream>
#include <set>
#include <vector>
using namespace std;
class binaryTree 
{
private:
	set<int> elemSet;  // 存放树中已有元素
	bool ifExistsElement(int elem);  // 是否存在一个元素
public:
	binaryTree() { }
	void createBST(binaryTreeNode * &root, vector<int> &v);  // 创建一个BST
	void inorder(binaryTreeNode *root);  // 中序遍历
	binaryTreeNode *insert(binaryTreeNode *root, int item);  // 插入
	binaryTreeNode *searchNode(binaryTreeNode *root, int value);  // 查找节点
	binaryTreeNode *leftRotation(binaryTreeNode *root, binaryTreeNode *node);  // 左旋
	binaryTreeNode *rightRotation(binaryTreeNode *root, binaryTreeNode *node);  // 右旋
	binaryTreeNode *maxValueNode(binaryTreeNode *root);  // 找到最小节点
	binaryTreeNode *minValueNode(binaryTreeNode *root);  // 找到最大节点
	binaryTreeNode *deleteNode(binaryTreeNode *root, int delete_item);   // 删除节点
};

插入节点

插入操作分两步：

  1. 找到要插入父节点的位置；
  2. 比较与该结点的大小，并插入。

如何找到要插入的父节点位置，这里我们可以使用递归较为方便；在做插入操作时需要注意的是，当树为空时，需要申请一个新节点，并将其作为结果返回。为什么不直接改变根节点的指向，让它直接指向新节点呢？那样就需要用到二级指针，复杂化原有的逻辑；这样做能保持方法实现的一致性，只不过在一棵树为空树时，插入节点后要获取其返回值才行；同时还需考虑节点是否重复。
⁃ 代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
/* 插入一个节点  */
binaryTreeNode *binaryTree::insert(binaryTreeNode *root, int item)
{
	// 检查是否元素重复
	if (ifExistsElement(item))
	{
		printf("element %d exists\n", item);
		return root;
	}
	
	if (root == NULL)  // （核心代码）
	{
		binaryTreeNode *temp = new binaryTreeNode(item);
		this->elemSet.insert(item);  // 插入已有元素集合
		return temp;
	}

	if (item > root->item)
		root->r_child = insert(root->r_child, item);
	else
		root->l_child = insert(root->l_child, item);

	return root;
}

通过以上代码我们可以看到，其实插入操作的真正核心就在第一个if (root == NULL)中。不管树的状态如何，程序最后都会走到这一步，然后再逐步返回。这也正是递归程序的真正意义，最后的结果永远会回到最终的地方，那里才是核心代码，其他都是为了走到那里的流程。

BST的创建

有了插入操作，创建BST就很简单了，我们可以把想放到树中的元素先放在一个vector里，然后逐个调用insert方法来构建BST.
代码如下：

1
2
3
4
5
6
7
8
9
10
11
/* 创建一颗二叉树 */
void binaryTree::createBST(binaryTreeNode* &root, vector<int> &v)
{
	if (v.empty())
		root = NULL;
	else
	{
		for (int val : v)  // 这里用到C++11的新标准，在编译时要注意
			root = insert(root, val);
	}
}

删除节点

删除节点稍显复杂，需要分情况讨论：

  1. 待删除节点没有孩子
  2. 待删除节点有一个孩子
  3. 待删除节点有两个孩子

对于前两种情况很简单，分别用NIL和该孩子节点替换删除节点，再删除待删除节点即可；

  • 情况一
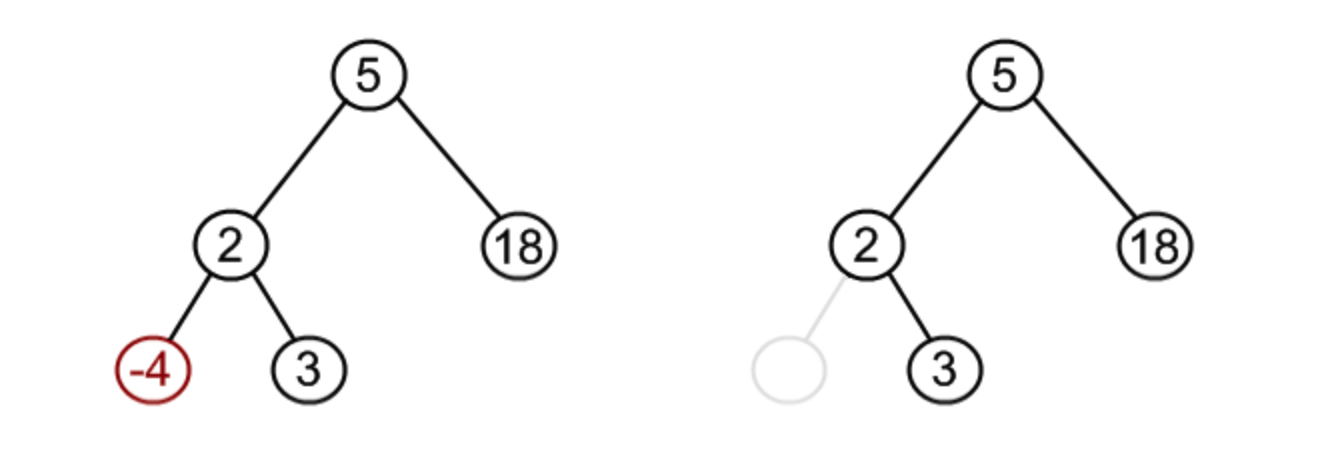
    satuation1

  • 情况二

    • 变化前

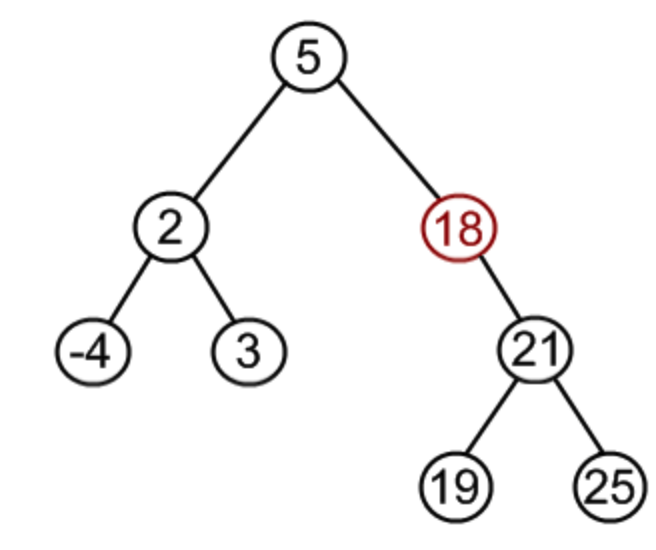
    • 变化后

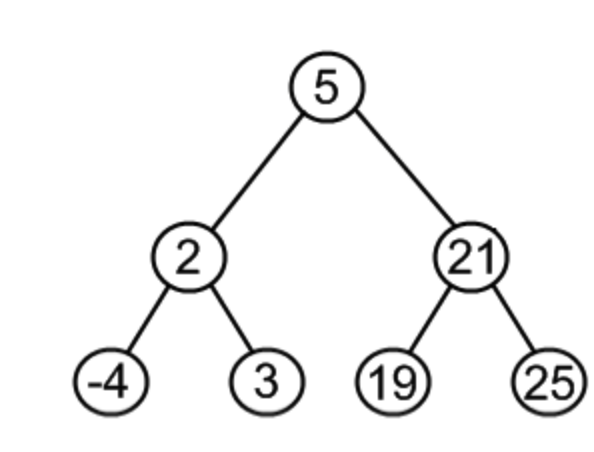
如果删除节点有两个孩子，这种情况可以找到删除节点的左孩子中最大节点、或右孩子中最小节点替换待删除节点，再释放删除节点。如下图，要删除12：

  • 情况三

    • 变化前

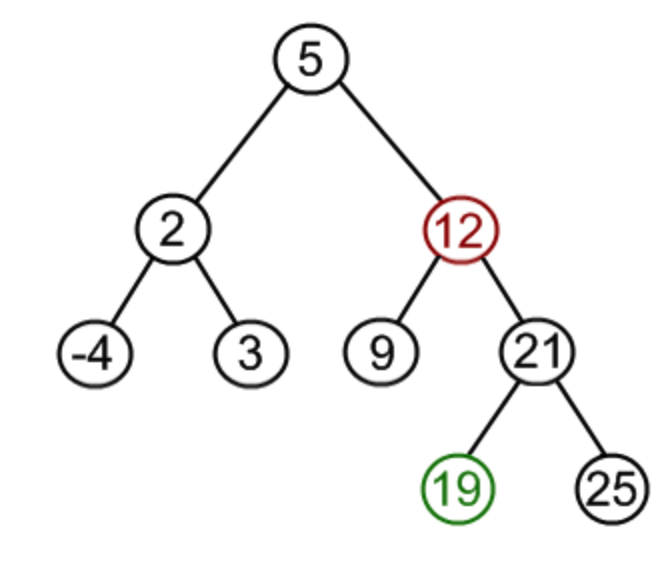
    • 变化后

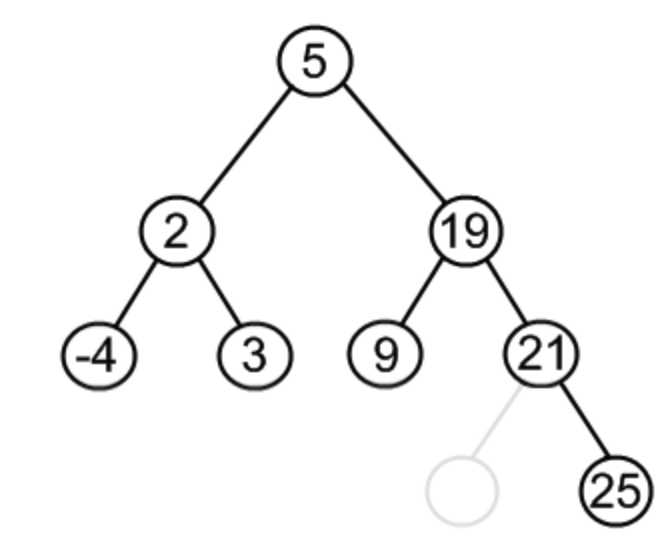
为什么可以这样做呢？正常的思路考虑就是：用左子树中最大节点替换根节点，由于它比所有左子树其他节点要大，而且比右子树中所有节点要小，故用其替换当前根节点不会使BST的性质发生变化；用右子树中最小节点也是同理。
和这个类似的操作还有二叉树的左旋的右旋，都利用了一个BST可以有多种呈现方式的特性。
实现代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
binaryTreeNode *binaryTree::deleteNode(binaryTreeNode *root, int value)
{
	if (root == NULL)  return NULL;

	if (value > root->item)
		root->r_child = deleteNode(root->r_child, value);
	else if (value < root->item)
		root->l_child = deleteNode(root->l_child, value);
	else
	{
		// 删除节点有一个孩子节点或无孩子节点（核心代码，最终调用的地方，然后再回调）
		if (root->l_child == NULL)
		{
			binaryTreeNode *temp = root->r_child;
			delete(root);
			return temp;
		}
		else if (root->r_child == NULL)
		{
			binaryTreeNode *temp = root->l_child;
			delete(root);
			return temp;
		}
		// 删除节点有两个孩子节点
		else
		{
			binaryTreeNode *leftChildMaxNode = maxValueNode(root->l_child);
			root->item = leftChildMaxNode->item;
			root->l_child = deleteNode(root->l_child, leftChildMaxNode->item);
		}
	}
	return root;
}

上面代码当删除节点有两个孩子时，首先用了左子树中最大节点替换了删除节点的内容，然后递归删除了左子树的最大节点，达到替换的目的。

其他一些功能方法

  • 找到BST的最大节点
    – 找一颗BST的最大节点就是找到其最深的右孩子节点，找到最小节点也是同理，即找到其最深的左孩子节点，便不再赘述。

代码如下：

1
2
3
4
5
6
7
binaryTreeNode *binaryTree::maxValueNode(binaryTreeNode *root)
{
	binaryTreeNode *cur = root;
	while (cur->r_child)
		cur = cur->r_child;
	return cur;
}
  • 判断一个元素是否已存在
1
2
3
4
5
6
7
8
9
10
/* 利用set的无重复元素的性质，判断一个元素是否在树中  */
bool binaryTree::ifExistsElement(int elem)
{
	for (auto pd = this->elemSet.begin(); pd != this->elemSet.end(); ++pd)
	{
		if (*pd == elem) 
			return true;
	}
	return false;
}
  • 中序遍历
    – 用递归的方法对一颗BST中序遍历（中根序遍历），中序遍历的结果是从小到大排好序的。
1
2
3
4
5
6
7
8
9
10
11
/* 中序遍历 */
void binaryTree::inorder(binaryTreeNode *root)
{
	if (root != NULL)
	{
		inorder(root->l_child);
		printf("%d \t", root->item);
		inorder(root->r_child);
	}
	else return;  // 可以不写，写了方便理解递归
}
  • 判断一棵树是否为二叉搜索树的方法（非类方法）
    – 要判断一颗二叉树树是不是BST，即要判断是否它的所有节点都满足：
    • 左孩子中最大的节点小于当前节点；
    • 右孩子中最小的节点大于当前节点；

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
/* 判断一棵树是否为二叉搜索树（BST）*/
bool ifIsA_BST(binaryTreeNode *root)
{
	binaryTree *tree = new binaryTree();
	if (root == NULL)
		return true;
	if (root->l_child != NULL && tree->maxValueNode(root->l_child)->item > root->item)
		return false;
	if (root->r_child != NULL && tree->minValueNode(root->r_child)->item < root->item)
		return false;
	if (!ifIsA_BST(root->l_child) || !ifIsA_BST(root->r_child))  // 递归做判断
		return false;
	return true;
}

这种方法不是最高效的，但比较容易理解，如果想了解更高效的方法，请参阅判断是否是BST的方法

  • 寻找一个节点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
/* 寻找一个节点，返回该节点的指针，没找到返回NULL */
binaryTreeNode *binaryTree::searchNode(binaryTreeNode *root, int value)
{
	if (root != NULL)
	{
		if (value == root->item)
			return root;
		else if (value > root->item)
			return searchNode(root->r_child, value);
		else if (value < root->item)
			return searchNode(root->l_child, value);
	}
	else return NULL;
}

测试程序

BST实现好了，下面来写代码测试它：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
int main()
{
	/* Let us create following BST 
     *         50 
     *      /     \ 
     *     30      70 
     *    /  \    /  \ 
     *  20   40  60   80 */
	binaryTreeNode *root = NULL;
	binaryTree *tree = new binaryTree();
	root = tree->insert(root, 50);
	tree->insert(root, 30);
	tree->insert(root, 20);
	tree->insert(root, 40);
	tree->insert(root, 70);
	tree->insert(root, 60);
	tree->insert(root, 80);
	tree->insert(root, 80);
	cout << "Inorder traverse tree1" << endl;
	tree->inorder(root);

	cout << endl << "max is " << tree->maxValueNode(root)->item << endl;

	cout << "delete 80" << endl;
	tree->deleteNode(root, 80);
	cout << "after delete" << endl;
	tree->inorder(root);

	cout << endl << "delete 30" << endl;
	tree->deleteNode(root, 30);
	cout << "after delete" << endl;
	tree->inorder(root);

	cout << endl << "second tree(create method)" << endl;
	binaryTreeNode *root1;
	vector<int> v{1,2,3,4,5,8,7};
	tree->createBST(root1, v);
	cout << "Inorder traverse tree2" << endl;
	tree->inorder(root1);

	if (ifIsA_BST(root1))
		cout << endl << "It's a BST." << endl;
	else
		cout << endl << "It's not a BST." << endl;

	return 0;
}

执行结果：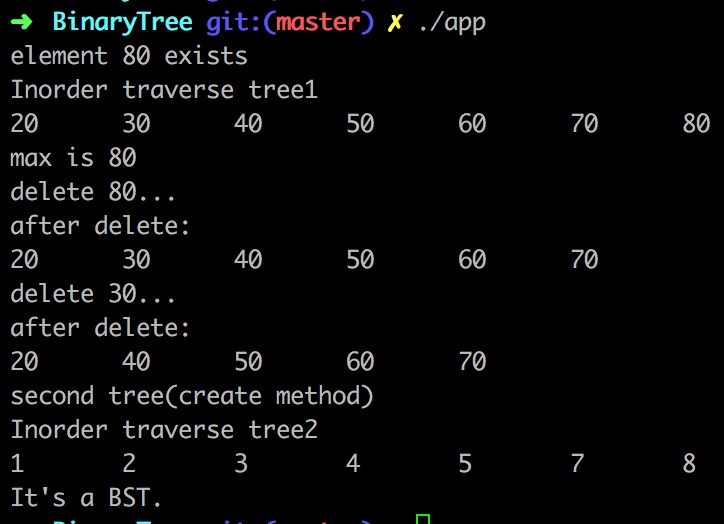

总结

以上对二叉搜索树（BST）的结构，性质，基本方法包括：创建、插入、删除、查找等，以及其他一些功能函数做了较为详细的分析，相信大家对BST已经有了更多的认识。
在学习BST的时候，递归是避免不了要理解的东西，想要理解递归，就要找到递归中最核心的代码部分，其余都是为了走向那里所做的流程处理，只不过是自己调用了自己，然后再从核心返回，一层一层调用回去。

参考链接

BST的基本操作
判断是否是BST的方法
一个很好的学习数据结构和算法的网站(左右旋转）