前言

动态规划（Dynamic Programming）这个词在大学的算法课上就曾学习过，但有多少人能真正把它掌握了呢？反正当时的我是一脸那啥的，光会死记硬背那些概念性的东西了。今天就让我们从一个实际问题出发，真正把动态规划的思想吃透。本文不会过多说明DP的概念，主要是结合最长公共子序列的问题用实例说明DP在解决问题上有什么优势，为什么用这种方法能提高效率。

最长公共子序列问题（Longest Common Subsequence）

最长公共子序列指的是两个字符串最长的相同部分，而不必是连续的。举个例子，有两个字符串A和B：

1 2	string A = "ABCD"; string B = "AKCD";

那么A和B的LCS为ACD。
最长公共子序列和最长公共子串的区别在于：子序列不必是连续的，而子串必须是，所以上例中的最长公共子串是CD。

一般思路

两种情况

解决LSC问题需要用到递归，这里用LCS（s1，s2）表示字符串s1和s2的最长公共子序列。还是上面的两个字符串A和B，要找到最长公共子序列，即LCS(“ABCD”, “AKCD”)，首先要比较两个字符串的第一个字符是否相同，这里显然是相同的，都是 'A', 这样二者的最长公共子序列就变成了：'A' + LCS(“BCD”, “KCD”);
接下来，'BCD', 'KCD'的首字母不同了，这种情况下要分别求出LCS(“CD”, “KCD”)和LCS(“BCD”, “CD”)，然后取二者中最长的那个作为结果。然后继续递归直到字符串为空，即可找出A和B的LCS了。

优化方法

不过需要优化的地方在于：每次计算子串的LCS时都要生成新字符串，这样很浪费空间，可以给LCS方法加两个参数i1，i2，分别表示指向s1，s2当前比较到的字符，如LCS(“ABCD”, “AKCD”, 0, 0)表示从头开始比较：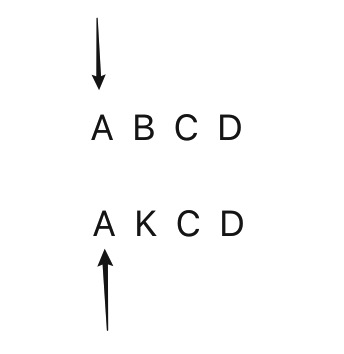

如此，便不难写出如下代码：

string LCS(string s1, string s2)
{
    string lcs = helper(s1, s2, 0, 0);
    return lcs;
}

string helper(string s1, string s2, unsigned long int i1, unsigned long int i2)
{
    // 如果字符串为空，直接返回空串
    if (s1.length() == i1 || s2.length() == i2) {
        return "";
    }


    // 如果比较的第一个字母相同，递归返回第一个字母加后面剩余的最长公共子序列
    if (s1[i1] == s2[i2]) {
        return s1[i1] + helper(s1, s2, i1 + 1, i2 + 1);
    }

    // 如果不同，返回下面两种结果中较长的一个
    string result;
    string resultA = helper(s1, s2, i1 + 1, i2);
    string resultB = helper(s1, s2, i1, i2 + 1);
    if (resultA.length() >= resultB.length())
        result = resultA;
    else
        result = resultB;
    return result;
}

存在问题

上述解法的确能够得到正确答案，但由于多次对相同的字符串进行递归计算LCS（既然这样，为什么我们不把中间计算过的结果记录下来呢？），从时间效率上来讲是很低的，在两个字符串很短的时候不会很明显，但如果一旦遇到两个稍长的字符串，等待时间将会很漫长，故这不是一种好的方法。如此我们便引入了动态规划，减少计算量，提高效率。

动态规划

为什么要用动态规划

我们可以看到，在求解LCS问题时，初始问题会转化成更小的“子问题”，而“子问题”的解决方法和初始问题以及子问题的子问题都是一样的，这种性质称之为 “重叠子问题” ，即是说每一个子问题并不是新的问题，而是解决方法完全一样的仅仅是规模不一样的问题；
另外，在求解LCS的过程中，能够利用相同字符连接上剩余字符串的最长公共子序列，这样来得到最终答案，这一性质又被称作 “最优子结构” ；
而具有以上两种性质的问题，最适合的算法就是“动态规划”，下面，我们就来用动态规划来对此问题进行优化。

动态规划算法的核心

有一句话很好地描述出了该算法的核心：

Those who cannot remember the past are condemned to repeat it.

在一位大牛的博客上看到过一个很形象的比喻：

A * "1+1+1+1+1+1+1+1 =？" *

A : "上面等式的值是多少"
B : *计算* "8!"

A *在上面等式的左边写上 "1+" *
A : "此时等式的值为多少"
B : *quickly* "9!"
A : "你怎么这么快就知道答案了"
A : "只要在8的基础上加1就行了"
A : "所以你不用重新计算因为你记住了第一个等式的值为8!动态规划算法也可以说是 '记住求过的解来节省时间'"

所以动态规划的核心就是把需要重复计算的耗时操作记录下来，即记录已经解决过的子问题的解。

优化代码

按照这个思路，我们可以对以上的代码进行如下优化。

定义一个二维的字符串数组memo，维数为s1.length() ✖️ s2.length()，将其添加到helper函数的参数中；
在每次计算LCS操作前，先到memo数组中找是否已经存在该结果，如果存在直接返回该结果，如果不存在，则先计算结果并把结果保存到memo相应的位置，再返回该结果。

这样一来，便可以省去很多重复计算子问题的时间。
下面是用动态规划方法优化后的代码：

string LCS(string s1, string s2)
{
    // 初始化一个二维string数组
    string **memo = new string*[s1.length()];
    for (unsigned long i = 0; i < s1.length(); ++i)
        memo[i] = new string[s2.length()];

    string lcs = helper_DP(s1, s2, 0, 0， memo);
    return lcs;  
}

string helper_DP(string s1, string s2, unsigned long int i1, unsigned long int i2, string **memo)
{
    // 如果字符串为空，直接返回空串
    if (s1.length() == i1 || s2.length() == i2) {
        return "";
    }

    // 如果结果已经在memo中，无需再次计算，直接返回
    if (!memo[i1][i2].empty())
        return memo[i1][i2];

    // 如果比较的第一个字母相同，递归返回第一个字母加后面剩余的最长公共子序列
    if (s1[i1] == s2[i2]) {
        memo[i1][i2] = s1[i1] + helper_DP(s1, s2, i1 + 1, i2 + 1, memo);
        return memo[i1][i2];
    }

    // 如果不同，返回下面两种结果中较长的一个
    string result;
    string resultA = helper_DP(s1, s2, i1 + 1, i2, memo);
    string resultB = helper_DP(s1, s2, i1, i2 + 1, memo);
    if (resultA.length() >= resultB.length())
        result = resultA;
    else
        result = resultB;
    // 先保存结果，再返回
    memo[i1][i2] = result;
    return result;
}

测试程序：

int main()
{
    string one = "I've been waiting for you for too long";
    string two = "I was waiting for you for so long";
    string lcs = LCS(one, two);
    cout << "It's " << lcs << endl;

    return 0;
}

运行结果：

注：利用动态规划的运行时间很快，但如果用第一种方法，运行这个需要计算很长时间，有兴趣的可以自己试一下。

总结

其实除LCS问题外还有很多类似可以用DP解决的问题，如Fibonacci数列某一项的值等，方法类似，再次不做赘述，有兴趣可移步Fibonacci数列的某一项。
在工作的过程中，由于基本都是一些业务流程上的开发，很少会用到算法，动态规划就更未曾使用过。但是算法在某些时候解决一些具有特定性质的问题时，确实是很有威力的，而一些看似很复杂的算法其实本质上都来源于生活中简单的道理，多了解一些算法，就相当于更了解生活，何乐而不为呢？

参考链接

CS Dojo
https://blog.csdn.net/u013309870/article/details/75193592